【奧數揭秘】同一題目問法多 舊瓶新酒細品味
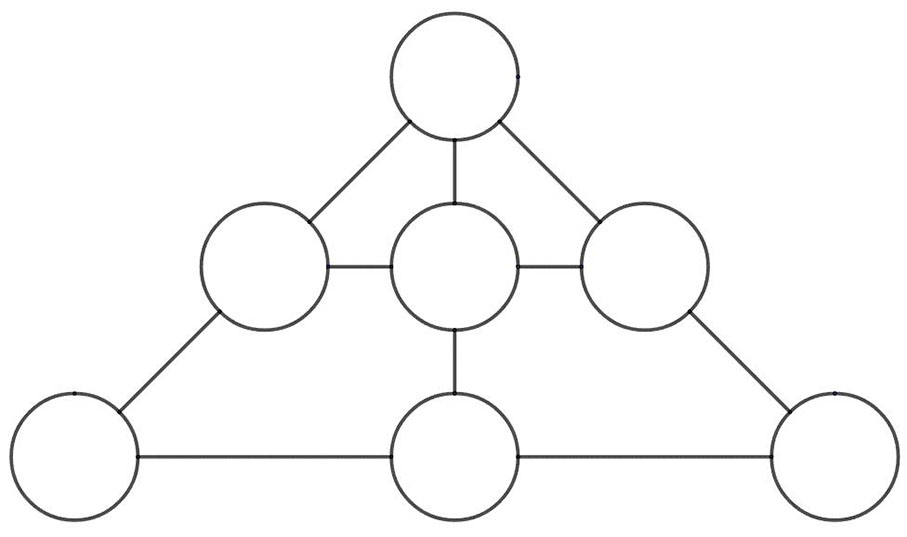

問題:圖一中共有七個圓圈,在圓裏填上1至7,每個數只能用一次,使得沿着各條直線上的三個數,共五個和都是一樣。那麼左下角的圓圈裏,不能填什麼數字?
答案:
考慮到1至7的總和是28,除了最上方的數,其餘6個數加起來的和記為P,這個P可以有兩種看法。
如圖二裏,三條線段標示了s的相鄰兩個圈裏的數,加上最上方的數,和都是一樣的,因此沒加上最上方的數,兩個圈裏的數的和都是一樣,這個和可記為s。故此P就是3s。
兩條橫線上各有三個圈,裏邊的數加起來,都是一樣的,可以記為t,故此P可記為2t。
因為P可以寫成3s和2t,因此是6的倍數,而28減去最上方的數,由於那數只能是1至7其中之一,減出來的差只能是24,而最上方的數只能是4,故此不可以出現在左下角。
其餘各數,留意到上下兩橫行是可以對調,也不影響各個和,另外,三條標示為s的線段相鄰的兩個圈分成一組時,三組也可以互換位置,又不影響總和。也就是說,4以外的數,可以出現在下方六個圈裏任何一個裏。
因此只有4不能出現在左下角。
這題做起來,看到除了上方那個數,其餘六個數有兩種看法,可以橫看和由上而下地看,橫向兩組,由上而下則有三組,從而找到其餘六個數是6的倍數,因此找到剛好小於28的24為六數之和,即最上方必為4,不能出現在左下角。
有時在小一小二的題目裏就有類似的問法,就是填個數字入圓圈那樣,試幾個情況,然後看看各線上加起來有沒有符合各個條件。對於初小來說,能寫到這樣已經不錯了,至少加法上是穩妥的,思考夠靈活,題目條件也理解正確。要是到了較高年班,能多列舉幾個情況出來,就更能歸納共通的法則。比如,看到上下兩橫行可以互換,或者直接全部列舉出來,水平就有所提高了。
若果學生可以在代數的層次上,去理解題目裏各組數加起來有什麼關係,從而找到當中的線索,比如最上方的數必定為4,過程中用了解方程組的方法,或者一些整數性質;比如整除性,或者其他數論知識,那又是層次更好的表現。若果還看到各樣互換關係,說得通下方其中一個數可以出現在任何位置,那又更好。
同一道題目,問法略作變化,就可以考察各個年級的解題能力。比如問初小,可以問他們找到一個同直線上總和一樣的填法,要是問起高中或初中,可以問他們有多少個不同的填法。若果問高中生,也就可以用這次的問法,問題看起來又多兩分陌生感。
在圓圈裏填數字,其實可以有多種變化,多花心思去推廣一下初等的問題,也可以有新發現。
◆ 張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
